حساب مساحة متوازي الأضلاع
2023-08-06 01:31:13 (اخر تعديل 2024-09-09 11:28:33 )
بواسطة طب 21 الشاملة
تعريف متوازي الأضلاع وخصائصه
متوازي الأضلاع هو شكل رباعي الأضلاع فيه كل ضلعين متقابلين متوازيين ويتميز بالخصائص الآتية:[1]
- كل ضلعين متقابلين في متوازي الأضلاع متساويين.
- كل زاويتين متقابلتين في متوازي الأضلاع متساويتين.
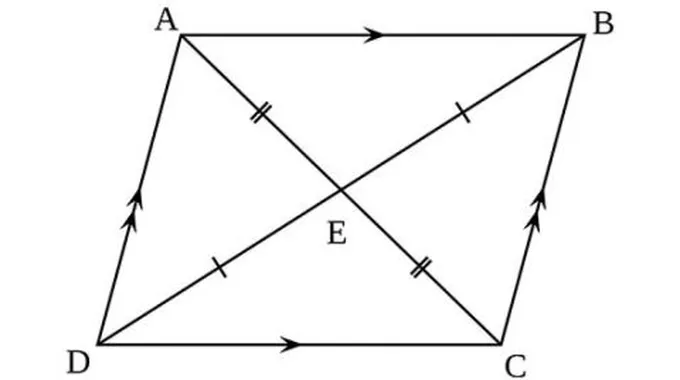
- أقطار متوازي الأضلاع تنصف بعضها عند نقطة التقاطع بين الأقطار.
- الفرق بين متوازي الأضلاع والمربع يكون في الأمور الآتية:[1]
- تكون جميع أضلاع المربع متساوية.
- تكون جميع زوايا المربع قائمة.
- تكون أقطار المربع متساوية ومتعامدة وينصف أحدهما الآخر.
حساب مساحة متوازي الأضلاع
يمكن حساب مساحة متوازي الأضلاع بعدة طرق:
- الطريقة الأولى: تستخدم هذه الطريقة إذا علم طول القاعدة والارتفاع، فتكون المساحة = طول القاعدة * الارتفاع.[2]
- الطريقة الثانية: تستخدم هذه الطريقة إذا علم ضلعا متوازي الأضلاع والزاوية المحصورة بينهما، وتكون المساحة = الضلع الأول * الضلع الثاني * جا(الزاوية)، وفي متوازي الأضلاع تكون كل زاويتين متجاورتين متكاملتين؛ أي مجموعهما 180°، لذلك يمكن استخدام أي زاوية لأن جا(الزاوية) = جا(180-الزاوية).[3]
أمثلة على حساب مساحة متوازي الأضلاع
من أمثلة حساب مساحة متوازي الأضلاع ما يأتي:[2]
- المثال الأول: متوازي أضلاع طول قاعدته 10 وارتفاعه 8 مامقدار مساحته؟
الحل: بتطبيق قانون مساحة متوازي الأضلاع فإن المساحة=8*10=80 وحدة مربعة.
- المثال الثاني: متوازي أضلاع طول قاعدته 3 وارتفاعه 6 مامقدار مساحته؟
الحل: بتطبيق قانون مساحة متوازي الأضلاع فإن المساحة=6*3=18وحدة مربعة.
- المثال الثالث: ما مقدار مساحة متوازي الأضلاع الذي يبلغ طول قاعدته 28 إنش (inch) وارتفاعه 24 إنش (inch) وطول أحد أضلاعه 31 إنش (inch)؟[4]
الحل: بتطبيق قانون مساحة متوازي الأضلاع فإن المساحة=28*24=672 إنش2.
محيط متوازي الأضلاع
محيط متوازي الأضلاع يساوي مجموع أطوال أضلاعه الأربعة، وذلك كما في المثال الآتي:[5]متوازي أضلاع طول ضلعيه: 10سم، 6 سم، ما مقدار محيطه؟
- بما أن كل ضلعين في متوازي الأضلاع متقابلين متساويين فإن طول الضلعين الآخرين هما 10سم و6 سم.
- وبالتالي فإن محيط متوازي الأضلاع= 10+6+10+6=32 سم
المراجع
- ^ أ ب Raghav Aggarwal (31-3-2018), "Properties of Parallelogram, Rhombus, Rectangle and Square"، www.toppr.com, Retrieved 8-2-2019. Edited.
- ^ أ ب "Area of parallelograms", www.khanacademy.org, Retrieved 8-2-2019. Edited.
- ↑ Hanna Pamuła, PhD student, "Parallelogram Area Calculator"، www.omnicalculator.com, Retrieved 8-2-2019. Edited.
- ↑ "Calculating The Area Of A Parallelogram", math.wonderhowto.com, Retrieved 8-2-2019. Edited.
- ↑ "Parallelograms: Area and Perimeter", www.varsitytutors.com, Retrieved 8-2-2019. Edited.














