قانون الجيب وقانون جيب التمام

2023-08-06 01:31:13 (اخر تعديل 2024-09-09 11:28:33 )

قانون الجيب

إنّ أي مثلث يتشكل من ثلاثة أضلاع والتي نرمز إليها ب: أ، ب، ج، حيث تكون الزوايا المقابلة لهذه الأضلاع هي: أَ، بَ، جَ، أما قانون الجيب فهو الذي يستخدم لمعرفة طول ضلعين مجهولين وزاوية من المثلث، وهو: أ/جا(أَ)=ب/جا(بَ)=ج/جا(جَ).[1]

قانون جيب التمام

يتكون المثلث من ثلاثة أضلاع رموزها هي: أ، ب، ج، ورموز الزوايا المقابلة لهذه الأضلاع هي أَ، بَ، جَ، ويربط بين هذه الاضلاع والزوايا قانون آخر بالإضافة إلى قانون الجيب هو قانون جيب التمام الذي يُستخدم لإيجاد طول ضلع ثالث لمثلث عُلمت أطوال ضلعيه الآخرين وقيمة الزاوية المحصورة بينهما، أو لإيجاد أطول أضلاع مثلث معلوم الزوايا، أما شكل قانون جيب التمام فهو: أ2=ب2+ج2-2ب ج جتا(أَ)، ب2=أ2+ج2-2أج جتا(بَ)، ج2=أ2+ب2-2أب جتا(جَ).[2]

يمكن ترتيب القوانين السابقة للحصول على القوانين التالية التي تستخدم لإيجاد قياسات زوايا المثلث مباشرة عند معرفة أطوال الأضلاع كالآتي: جتا (جَ)=(أ2+ب2-ج2)/2أب، جتا (بَ)= (ج2+أ2-ب2)/2أج، جتا (أَ)= (ب2+ج2-أ2)/2ب ج.[2]

أمثلة على قانون الجيب وجيب التمام

مثال على قانون الجيب:

يوضح المثال الآتي طريقة إيجاد طول ضلعين مجهولين في مثلث أحد أضلاعه معلوم، وزاويتين من زواياه معلومة.[1]

المثلث أ ب ج فيه الضلع أب=9سم، والزاوية أب ج=76 درجة، والزاوية أج ب=58 درجة، احسب مع التقريب إلى أقرب منزلتين طول الضلعين أج، وب ج؟

حساب قيمة أج باستخدام قانون الجيب: حيث أج/جا (76)=9/جا(58)، ومنها أج=9*جا(76)/ جا(58)=10.30سمحساب قيمة ب ج بعد إيجاد قيمة الزاوية ج أ ب حيث يساوي مجموع زوايا المثلث 180 درجة، ومنها: 180-76-58=46 درجة، ثمّ حساب قيمة ب ج باستخدام قانون الجيب حيث ب ج/جا(46)=9/ جا(58) ومنها ب ج=7.63سم تقريباً

حساب قيمة ب ج بعد إيجاد قيمة الزاوية ج أ ب حيث يساوي مجموع زوايا المثلث 180 درجة، ومنها: 180-76-58=46 درجة، ثمّ حساب قيمة ب ج باستخدام قانون الجيب حيث ب ج/جا(46)=9/ جا(58) ومنها ب ج=7.63سم تقريباً

أمثلة على قانون جيب التمام:

المثال الأول:

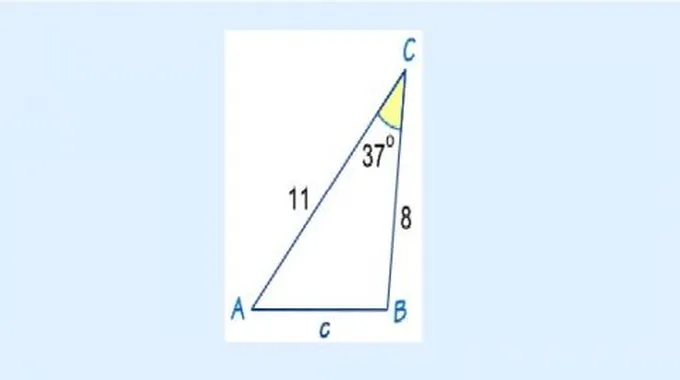
يوضح المثال الآتي طريقة إيجاد طول ضلع مفقود في مثلث ضلعيه الآخرين معلومين، والزاوية المقابلة لهذا الضلع المجهول معلومة.[2]

احسب طول الضلع ج في مثلث فيه الضلع أ=11، والضلع ب=8، والزاوية المقابلة للضلع ج(جَ)=37 درجة؟

باستخدام قانون جيب التمام: ج2=أ2+ب2-2أب جتا(جَ)=28+211-2*8*11* جتا (37)=64+121-176*0.798=44.44، ومنها ج=الجذر التربيعي (44.44)=6.67 بالتقريب إلى أقرب منزلتين

المثال الثاني:

يوضح المثال الآتي طريقة إيجاد قيمة طول ضلع مجهول لمثلث غير قائم الزاوية باستخدام قانون جيب التمام:[3]

احسب قيمة الضلع الثالث في المثلث ف د ي، حيث يبلغ طول الضلع د ي=15.24سم، والضلع ف ي =17.78سم، والزاوية د ي ف=95 درجة؟

باعتبار الزاوية د ي ف هي الزاوية جَ، أ=15.24سم، ب=17.78سم، وباستخدام قانون جيب التمام: ج2=أ2+ب2-2أ ب جتا(جَ)=215.24+217.78-2*17.78*15.24*جتا (95) ومنها ج=الجذر التربيعي(595.62)=24.4سم.

المراجع

^ أ ب "The sine and cosine rules"، www.amsi.org.au، Retrieved 28-10-2017. Edited.
^ أ ب ت "The Law of Cosines"، www.mathsisfun.com، Retrieved 28-10-2017. Edited.
↑ "Using the Law of Cosines to Find the Third Side"، www.softschools.com، Retrieved 31-10-2017. Edited.