مساحة شبه المنحرف القائم

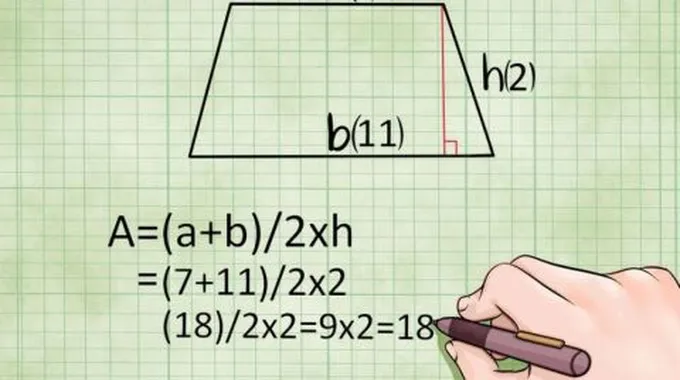
شبه المنحرف القائم

شبه المنحرف هو شكلٌ هندسيٌ رباعيٌ مجموع زواياه يساوي 360 درجة، فيه ضلعان متقابلان متوازيان ولا يعتبر متوازي الأضلاع شبه منحرف لأن فيه كل ضلعين متقابلين متوازيين ومتساويين وهذا لا ينطبق على شبه المنحرف.

شبه المنحرف شكلٌ ثنائي الأبعاد فيه ضلعان يسميان بالقاعدتين وهما المتوازيان، وفيه الضلعان الباقيان يسميان بالساقين، وهناك أنواعٌ من شبه المنحرف وكلٌ نوع منها له قوانين خاصةٍ بالمساحة والمحيط.

أنواع شبه المنحرف

• شبه المنحرف العام: وهو شبه المنحرف الذي يكون فيه ضلعان متوازيان غير متقايسين، وقطراه غير متقايسين و يتقاطعان في نقطة، و ارتفاعه هو البعد بين الضّلعين المتوازيين، فيه مجموع كل زاويتتين متتاليتن يساوي 180 درجة.
• شبه المنحرف متقايس الضّلعين: يكون فيه ضلعان متوازيان غير متقايسين، وضلعان متقايسان غير متوازيين، وقطراه متقايسان ويتقاطعان في نقطةٍ، وفيه مجموع كل زاويتين متتاليتين يساوي 180 درجة.
• شبه المنحرف القائم الزّاوية: وهو الذي يكون فيه زاويتان قائمتان ( الزاوية القائمة هي التي يكون قياسها 90 درجة)، وارتفاعه هو العمود النازل على القاعدة الكبرى، وسنتكلم اليوم عن هذا النوع من شبه المنحرف ونشرح قوانين المساحة والمحيط الخاصة به.

مساحة شبه المنحرف القائم الزاوية

مساحة شبه المنحرف القائم الزاوية تحسب بجمع القاعدتين وضربها في الارتفاع ثم قسمة الكل على العدد2، ورياضياً:

مساحة شبه المنحرف=1/2×مجموع القاعدتين×الارتفاع.

• مثال1: شبه منحرفٍ قائم الزاوية، فيه طول القاعدة الكبرى يساوي 10سم، وطول القاعدة الصغرى يساوي 5سم، وارتفاعه 7سم، احسب مساحته.

• مثال2: شبه منحرفٍ قائم الزاوية مساحته 75سم²، وطول قاعدته الكبرى 8سم، وارتفاعه 10سم، احسب طول قاعدته الصغرى.

مساحة شبه المنحرف=1/2×مجموع القاعدتين×الارتفاع.

• مثال3: شبه منحرفٍ قائم الزاوية محيطه يساوي 28سم، إذا كان طول القاعدة الكبرى فيه يساوي 5سم، وارتفاعه يساوي 7سم، ومساحته تساوي 45.5سم²، احسب مجموع طولي الساقين.

مساحة شبه المنحرف=1/2×مجموع القاعدتين×الارتفاع.

• مثال4: رسمت طالبةٌ شبه منحرفٍ قائمٍ على اللوح، فكانت مساحته 125سم²، وكان ارتفاعه 10سم، وكان طول الساقين 7سم و9سم على التوالي، احسب محيط شبه المنحرف.

مساحة شبه المنحرف=1/2×مجموع القاعدتين×الارتفاع.

محيط شبه المنحرف القائم=مجموع القاعدتين+مجموع طولي الساقين