ما هو نصف قطر الدائرة
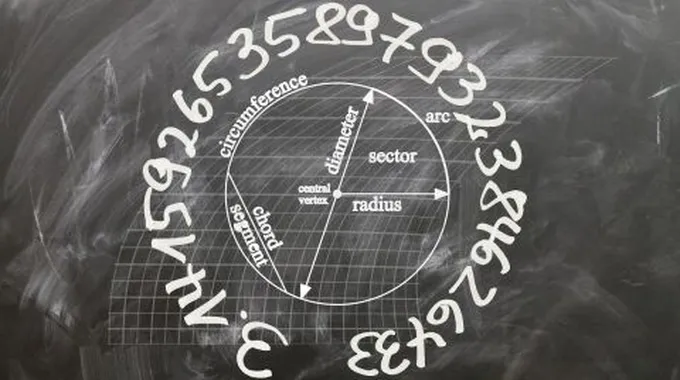
نصف قطر الدائرة
الدائرة هي شكل مُستدير تماماً بشكل مثالي، ولكل دائرة مركز يقع في مُنتصفها، ويُمكن القول بأن الدائرة هي أي شكل تكون فيه المسافة بين مركزها وأي نقطة على حوافها ثابتة وذات قيمة واحدة، وتُسمى هذه المسافة الواصلة بين مركز الدائرة وأي نقطة على حافة الدائرة نصف القطر، بينما يُعرف قطر الدائرة بأنه المسافة الواصلة بين أي نقطتين على محيط الدائرة بشرط مرورها في مركز الدائرة، وبالتالي فإن القطر يُساوي نصف القطر مضروباً بالعدد 2، ومن المصطلحات المتعلقة بالدائرة أيضاً المحيط، حيث إن محيط دائرة ما يدل على المسافة الخارجية حول الدائرة.[1]
حساب نصف قطر الدائرة
باستخدام محيط الدائرة
يمكن استخدام قيمة محيط الدائرة إذا عُرفت لحساب قيمة نصف قطر الدائرة، وينص قانون محيط الدائرة على أن:[2]
المحيط= 2×π×نق
حيث إنّ نق ترمز إلى نصف قطر الدائرة، وπ قيمة ثابتة تساوي تقريباً 3.14.
باستخدام المعادلة السابقة فإن نق= المحيط÷(2*π)، وبالتالي فإنه يمكن إيجاد قيمة نصف القطر إذا عُرف المحيط لها.
باستخدام مساحة الدائرة
يمكن حساب نصف قطر دائرة ما باستخدام مساحتها، حيث إن قانون مساحة الدائرة يساوي:[3]
المساحة= π × نق²
على سبيل المثال لو أن دائرة تبلغ مساحتها 50.24 م²، فإن نصف قطرها يمكن إيجاده باتباع الخطوات الآتية:
المساحة=π×نق²نق²=50.24÷3.14نق²= 16نق =16 √نق= 4 م²
باستخدام الزاوية المركزية للقطاع الدائري
ينص قانون مساحة القطاع الدائري لدائرة ما على أن:[2]
مساحة القطاع الدائري=نق²×π×(هـ/360)
حيث إنّ: نق هو نصف قطر الدائرة، π هو الثابت الرياضي الذي تبلغ قيمته 3.14، هـ هي الزاوية المركزية للقطاع بالدرجات.
فعلى سبيل المثال لو كان هناك دائرة يبلغ مساحة قطاعها 50م²، وزاوية قطاعها 120 درجة، فإن نصف قطرها يساوي:
مساحة القطاع الدائري=نق²×π×(هـ/360)50=نق²×3.14×(120÷360)نق²=(50×360)÷(3.14×120)نق²= 18000÷ 376.8نق²= 47.77نق²= 6.9م، وبالتالي فإن نصف القطر الدائرة السابقة يساوي 6.9 م.
المراجع
- ↑ "Radius, diameter, & circumference", www.khanacademy.org, Retrieved 11-5-2019. Edited.
- ^ أ ب "How to Calculate the Radius of a Circle", www.wikihow.com, Retrieved 11-5-2019. Edited.
- ↑ "How to Calculate Radius", www.sciencing.com,3-5-2018، Retrieved 11-5-2019. Edited.














