قانون حساب حجم المخروط
تعريف المخروط
يُعرف (المخروط: بالإنجليزية Cone) على أنه مجسّم يحتوي على قاعدة واحدة فقط مسطحة ودائرية الشكل، كما أنه يتكون من دوران مثلّث قائم الزاوية بحيث يدور حول أحد ضلعيه الأقصر من الوتر، فيتشكّل سطحه المنحني من الجوانب، أما النقطة المدبّبة الموجودة أعلى هذا المجسم فتُسمّى برأس المخروط.[1] وبمعنى آخر، المخروط هو عبارة عن هرم ذي قاعدة منحنية وليست مضلعاً (ليس له جوانب)، فإذا كانت قاعدته دائرية سُمي بالهرم الدائري.[2]
خصائص المخروط
إن للمخروط -كغيره من الأجسام الهندسية- مجموعة من الخصائص التي تميزه عن غيره ومن بعض هذه الخصائص ما يأتي:[2][1]
- يحتوي المخروط على قاعدة واحدة مسطّحة الشكل.
- يتكون المخروط من جانب منحنٍ واحد.
- يعد المخروط ذا أبعاد ثلاثية (مجسم).
قانون حجم المخروط
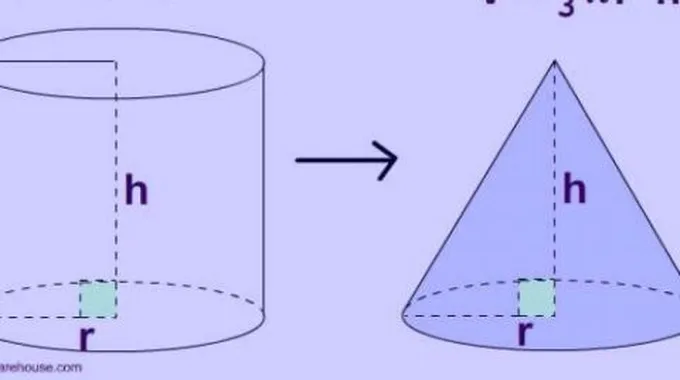
في حال تمّ إحضار مخروط وأسطوانة يشتركان في القاعدة والارتفاع، حيث طُلب ملء الأسطوانة الموجودة بالتراب وذلك عن طريق استخدام المخروط، فسيلاحظ بأن الأسطوانة ستمتلئ بالتراب بعد ثلاث مرات من تعبئة المخروط ووضعه بالأسطوانة، وبناءً عليه يستنتج بأن: (حجم الأسطوانة يساوي ثلاثة أمثال حجم المخروط المشترك معها بالارتفاع والقاعدة).[3]
أمثلة تبيّن كيفية حساب حجم المخروط
- (مثال1): أوجد حجم شكل مخروطي إذا علمت أن نصف قطر قاعدته يساوي 11سم، وارتفاعه يساوي 16سم؟
- (مثال2): أوجد حجم شكل مخروط دائري قائم، إذا علمت أنه يشترك مع أسطوانة دائرية في الارتفاع ونصف قطر القاعدة، وكان حجم الأسطوانة يساوي 3360دسم³.[3]
- (مثال3): احسب حجم المخروط الدائري القائم الذي قطر قاعدته يساوي24 م، وارتفاعه يساوي 15م؟[3]
- (مثال4): أسطوانة دائرية قائمة، قطر قاعدتها يساوي 20سم، يعلو هذه الأسطوانة مخروط دائري قائم مشترك مع الأسطوانة في الارتفاع نفسه، فإذا علمت أن طول راسمه يساوي 30 سم، جد حجم المجسم بالكامل.[3]
مساحة المخروط
يتكوّن المخروط القائم من قطاع دائري، حيث إن مساحة القطاع الدائري تعبر عن المساحة الجانبية للمخروط القائم، أما القاعدة فهي عبارة عن شكل دائري، ولحساب المساحة الكلية للمخروط القائم يجب حساب مساحة الجانب ومساحة القاعدة.[3]
وبهذا فإن:[3]
ومن الممكن استخدام القانون الآتي لحساب المساحة الجانبية للمخروط وهي:[3]
وفيما يأتي مثال يبين كيفية حساب مساحة المخروط الدائري.
- مثال: كرتونة على شكل نصف دائرة، قطرها يساوي 3سم، فإذا علمت أنه تم تحويلها لمخروط قائم أجوف، احسب المساحة الجانبية لهذا المخروط؟
المراجع
- ^ أ ب "Cone", www.mathsisfun.com, Retrieved 2-1-2018. Edited.
- ^ أ ب رجائي سميح العصار، جواد يونس أبو هليل،محمد زهير أبو صبيح (2013)، مدخل إلى أولمبياد ومسابقات الرياضيات (الطبعة الأولى)، الرياض: جامعة الملك فهد للبترول والمعادن عمادة البحث العلمي_ مكتبة العبيكان، صفحة 86. بتصرّف.
- ^ أ ب ت ث ج ح خ شادية غرايبة، معن المومني، ياسمين نصير. (2007)، دليل المعلم الرياضيات الصف الثامن (الطبعة الأولى)، الأردن-عمان: وزارة التربية والتعليم إدارة المناهج والكتب المدرسية، صفحة 138-142 ملف128-155، ملف اجابات الاسئلة 199-217، جزء الثاني. بتصرّف.














