مساحة الشبه المنحرف
المُضلّع
المُضلع هو شكل هندسي مغلق يحتوي على ثلاث قطع مستقيمة أو أكثر من ذلك، حيث تتقاطع كل قطعتين مستقيمتين لتشكل نقطة التقاء تسمى برأس المضلع، ومن الأمثلة على المضلعات، المربع والمستطيل، والمثلث، ومتوازي الأضلاع و شبه المنحرف وغيرها من الأشكال الهندسية.[1]
المضلع الرباعي هو شكل هندسي مُغلق يحتوي على أربعة أضلاع فقط، مجموع أطوال هذه الأضلاع تُمثل محيط المضلع،أما أقطار المضلع الرباعي فهي عبارة عن القطعة المستقيمة الواصلة بين كل زاويتين غير متجاورتين، حيث تقوم على تجزئة الشكل إلى جزأين يمثل كل منهما مثلث، وبما أن مجموع قياس الزوايا الداخلية للمثلث الواحد تساوي 180 درجة، إذن مجموع زوايا الشكل الرباعي تساوي 360 درجة، ومن الأمثلة على الأشكال الهندسية التي تُمثل مضلعات، المربعات والمستطيلات واشباه المنحرفات، ومتوازيات الأضلاع، أما المثلثات فتستبعد من قائمة المضلعات الرباعية لأنها ثلاثية الأضلاع.[1]
شبه المنحرف
شبه المنحرف (بالإنجليزية: Trapezoid) هو أحد أهم الأشكال الهندسية الرباعية (التي تحتوي على أربعة جوانب)، فيه زوج واحد فقط من الجوانب المتوازية، وهما يمثلان قاعدتيْ شبه المنحرف، أما ارتفاع شبه المنحرف فهو عبارة عن المسافة العمودية بين القاعدتين، في حين أن الزوج الآخر من الجوانب غير متوازية، يمثلان ساقي شبه المنحرف، فإذا تطابق الساقين حينها يسمى شبه المنحرف بمتساوي الساقين، وبما أن الساقين متطابقين فإن زوايا القاعدة بالتاكيد متساوية، وبالتالي فإن قطري شبه المنحرف أيضاً متطابقين.[1][2]
أنواع شبه المنحرف
هناك ثلاثة أنواع من شبه المنحرف، أوّلها شبه المنحرف الذي لا تتطابق ساقاه، وليس فيه أيّ ساقٍ عمودية على القاعدتين، أما النوعان الآخران فهما:[2]
- شبه المنحرف القائم الزاوية: وهو شبه المنحرف الذي أحد ساقيه (ساق على الأقل) عمودياً على القاعدتين.
- شبه المنحرف المتساوي الساقين: وهو شبه المنحرف الذي ساقيه متطابقين ومتساويين، وبناءاً على تساوي الساقين فإن زوايا القاعدة أيضاً متطابقة.
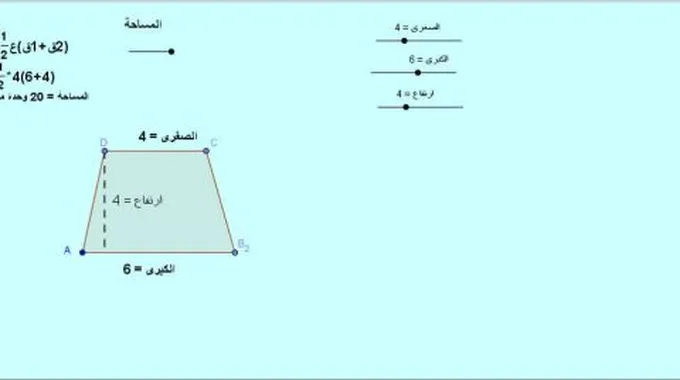
مساحة شبه المنحرف
يوجد عدة طرق لحساب مساحة شبه المنحرف وهي عبارة عن المنطقة الداخلية التي تقع ضمن حدودها ومنها:[3]
- إحدى الطرق البسيطة التي يمكن من خلالها ايجاد صيغة مساحة شبه المنحرف هي رسم شبه منحرف مطابق لشبه المنحرف الموجود ومن ثم قلبه والصاقه بجانب الشكل الأول، حينها سينتج من التصاق الشكل الأول مع الشكل الثاني متوازي أضلاع ، فيه مساحة شبه المنحرف الأول= مساحة شبه المنحرف الثاني.
أمثلة على حساب مساحة شبه المنحرف
ومن الأمثلة التوضيحية التي تبين كيفية حساب مساحة شبه المنحرف ما يلي:
- مثال1: شبه منحرف، فيه طول القاعدة الأولى=4سم، وطول القاعدة الثانية= 6سم، أما ارتفاعه= 3سم، فجد مساحته.[5]
- مثال2: ساحة على شكل شبه منحرف مساحتها تساوي 200 م، إذا علمت أن مجموع طولي قاعدتها يساوي20 م، احسب ارتفاعها.[3]
- مثال3: شبه منحرف، فيه مجموع طولي القاعدتين يساوي62 دسم، أما ارتفاعه فيساوي 18 دسم، احسب مساحة شبه المنحرف.[6]
- مثال4: شبه منحرف، فيه طول القطعة المتوسطة يساوي 12سم، أما ارتفاعه فيساوي 10سم، احسب مساحته.
محيط شبه المنحرف
محيط أي شكل هندسي هو عبارة عن مجموع قياسات حوافه، إذن محيط شبه المنحرف يساوي طول الحافة الاولى+ طول الحافة الثانية+ طول الحافة الثالثة+ طول الحافة الرابعة. وبالتالي فإن محيط شبه المنحرف يساوي مجموع أطوال حوافه.[5]
أمثلة على حساب محيط شبه المنحرف
من الأمثلة التوضيحية التي تبين كيفية حساب محيط شبه المنحلرف ما يلي:
- مثال1: بِساط على شكل شبه منحرف، فيه طول حوافه الأربعة على التوالي،5 م، 15م، 12م، 4 م، فجد مساحته.[5]
- مثال2: ورقة على شكل شبه منحرف، إذا علمت أن طول حوافها الأربعة على التوالي،2سم، 1سم، 3 سم، 1.5سم، فجد مُحيط الورقة.
- مثال3: لوح خشبي على شكل شبه منحرف، أذا علمت أن طول حوافه الأربعة على التوالي،14سم،10سم، 13سم، 9سم، فجد مُحيط اللوح الخشبي.
المراجع
- ^ أ ب ت رجائي سميح العصار، جواد يونس أبو هليل،محمد زهير أبو صبيح (2013)، مدخل إلى أولمبياد ومسابقات الرياضيات (الطبعة الأولى)، الرياض: جامعة الملك فهد للبترول والمعادن عمادة البحث العلمي_ مكتبة العبيكان، صفحة 63-88. بتصرّف.
- ^ أ ب معروف سمحان،نجلاء التويجري،ليان توبان (2016)، رياضيات الأولمبياد: الهندسة (الطبعة الأولى)، الرياض: مؤسسة الملك عبد العزيز للموهبة والإبداع،العبيكان، صفحة 155-180، جزء الأول. بتصرّف.
- ^ أ ب باجس خمايسة، ابراهيم الصماي، فدوى الحشاش (2007)، دليل المعلم الرياضيات الصف الخامس (الطبعة الأولى)، الأردن-عمان: وزارة التربية والتعليم إدارة المناهج والكتب المدرسية، صفحة 108-112ملف(5)، جزء الأول. بتصرّف.
- ^ أ ب ت "Area of a trapezoid", www.mathopenref.com, Retrieved 17-1-2018. Edited.
- ^ أ ب ت "Trapezoid", www.mathsisfun.com, Retrieved 22-12-2017. Edited.
- ↑ "Area-and-Perimeter-of-Trapezoids", www.ck12.org, Retrieved 22-12-2017. Edited.














