ما هو قانون مساحة المثلث

المُثلث

يُمكن تعريف المثلث رياضياً على أنَّه شكل هندسي مُضلَّع ثُلاثيّ الجوانب، يُمكن تَصنيفه على حَسب الزوايا الخاصة به، كالمثلث الحاد، أو المثلث مُتساوي الأضلاع، ويكون مجموع زوايا المُثلث دائماً 180 درجة.[1]

قانون مساحة المثلث

يُوجد العديد من الطُّرُق والقوانين المُستخدمة في عملية حِساب مساحة المُثلث، ومنها:[2]

• القانون الأساسي لِحساب مَساحة المُثلث: حَيث يَنُص هذا القانون على أنَّ مَساحة المُثلث تُساوي نِصف طول قاعدة المُثلث مَضروباً بارتفاع هذا المُثلث.
• قانون هيرون لِحساب مَساحة المُثلث: يَحسِب قانون هيرون مَساحة المثلث من خلال استخدام أطوال أضلاعه الثلاث، فإذا فرضنا أن مَساحة المُثلث رمزُها "م"، فإنَّ (م = (س*(س- أ)*(س- ب)*(س -ج))½) حيث إن أطوال أضلاع المُثلث الثلاث هي أ، وب، وج ، أمَّا عن س فهو عِبارة عن نصف مُحيط المُثلث، ويُساوي (س=(أ +ب+ ج)/2).
• الصيغة العامة لِحساب مَساحة المُثلث: وهذه الصيغة هي الصيغة المُستخدمة في إثبات قانون الجيب أيضاً، وهي كالتالي (م= ½ *أ *ب *جا(ج))، حيث إن م هي رمز مساحة المُثلث، و ضلعا المُثلث هما الضلع أ، والضلع ب، أمّا عن ج فهي الزاوية الخاصة بالضلع ج، وجا هو اختصار لجيب الزاوية.

أمثلة على حساب مساحة المُثلث

فيما يلي بعض الأمثلة على حساب مساحة المُثلث، سيتم الحل بتطبيق القانون الأساسي لحساب مَساحة المُثلث والذي ينص على أنَّ مساحة المُثلث تُساوي نصف طول القاعدة الخاصة بالمثلث مَضروبة بارتفاعه:[3]

• المِثال الأول: إذا تواجد لدينا مُثلث طول قاعدته تساوي 4 سم، وارتفاعه يُساوي 5 سم، ما هي قيمة مساحته؟

• المِثال الثاني: يوجد مُثلث طول قاعدته تُساوي 8 سم، وطول أحد أضلاعه يُساوي 5 سم، أمَّا عن ارتفاعه فهو 4 سم، فما هي قيمة مساحته؟

• المِثال الثالث: مُثلث قائم الزاوية، طول ضلعه القائِم يُساوي 5 سم، وطول قاعدته تُساوي 6 سم، فما هي قيمة مساحته؟

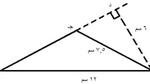
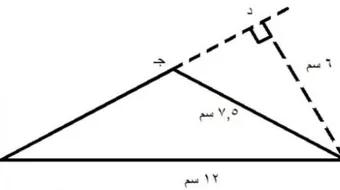
• المِثال الرابع: مُثلث مساحة قاعدته تُساوي 4 سم، والبُعد بين رأسه العلوي والزاوية القائِمة المصنوعة مع الخط السُفلي لِضِلعَيه تُساوي 5 سم، فما هي قيمة مساحته؟

فيما يلي بعض الأمثلة على حساب مساحة المُثلث، سيتم الحل بتطبيق قانون هيرون لحِساب مَساحة المُثلث:[4]

• المِثال الأول: يوجد مُثلث طول ضلعه الأول يساوي 16 م، وطول ضلعه الثاني يُساوي 22 م، وطول ضلعه الثالث يُساوي 12 م، فما هي قيمة مساحته؟

• المِثال الثاني: يوجد مُثلث طول ضلعه الأول يساوي 10 م، وطول ضلعه الثاني يُساوي 6 م، وطول ضلعه الثالث يُساوي 8 م، فما هي قيمة مساحته؟

• الحل: محيط الُمثلث يُساوي مجموع أطوال أضلاعه، ح=10+6+8= 24، ونصف مُحيطه يُساوي 12، إذاُ فإنَّ مَساحة المُثلث تُساوي (م = (12*(12- 10)*(12-6)*(12 -8))½)، ومنها فإنَّ مساحة المُثلث تُساوي 24م2.

مصطلحات خاصة بالمثلث

يُمكن تعريف بعض المُصطلحات الخاصة بالمثلث خلال ما يلي:[5]

• رأس المُثلث (بالإنجليزية: vertex of a triangle): يُمكن تعريف رأس المثلث على أنها النًقطة التي يلتقي بها ضِلعيّ المُثلث.
• ارتفاع المُثلث العامودي (بالإنجليزية: altitude of a triangle): إن ارتفاع المُثلث العامودي هو المَسافة العاموديَّة من قمة المثلث إلى الضلع المقابل لقمَّته.
• قاعدة المُثلث (بالإنجليزية: base of a triangle): السطح المُقابل لِقمة المُثلث، والذي يتم أخذ الارتفاع منه.
• ارتفاع المًثلث (بالإنجليزية: height of a triangle): هو نفسه ارتفاع المُثلث العامودي.

المراجع

1. ↑ "triangle", www.thefreedictionary.com, Retrieved 28-4-2019. Edited.
2. ↑ "Area of a Triangle", www2.clarku.edu/, Retrieved 27-4-2019. Edited.
3. ↑ "Area of triangles", www.khanacademy.org, Retrieved 28-4-2019. Edited.
4. ↑ " Area of a Triangle - Heron's Formula", www.softschools.com/, Retrieved 28-4-2019. Edited.
5. ↑ "The Area of a Triangle", www.geom.uiuc.edu/, Retrieved 28-4-2019. Edited.