كيف نحسب مساحة المستطيل
المستطيل
عِلم الحساب هو من أقَدم العُلوم التي عَرفها الإنسان ومن أهمّها؛ لأنه يُستَخدم دائماً في جميع مجالات الحياة ولا يُمكن الاستغناء عنه. تعدّ الأشكال الهندسية كثيرة ومنها المُربّع، والمستطيل، والمثلث، والمَعين، والدائرة، وغيرها العديد من الأشكال. يُعرَّف المُستطيل (بالإنجليزية: Rectangle) بأنَّه شكلٌ هندسيّ مُنتظم مُكوَّن من أربعة أضلاع، كلّ ضلعين مُتقابلين فيه متساويان في الطول، والزاوية بين كلّ ضِلعين من أضلاعه قائمة أي تساوي 90°.[1]
تَكمُن أهميّة حِساب مساحة المستطيل في أنّها مَوجودة في كلّ حياة الإنسان؛ ففي حال أراد شخص أن يَفرش مَنزله بالسجّاد يجب عليه أن يُحدّد مساحات الغرف في منزله ومعرفة كم مساحة السجّاد المُستخدم في تغطية البيت كاملاً ليَعرف مقدار التكلُفة، وكذلك لو رغب أحد في تصميم طاولة أو مكتب أو أيّ شيء من أثاث البيت يجب عليه مَعرفة مِقدار المساحة المتوفّرة لدية بدايةً قبل الشراء أو التركيب.[2]
خصائص المستطيل
للمستطيل خصائص عدة أهمّها:[1][3]
- يحوي المستطيل على بُعدين فقط هما: الطول والعرض.
- جميع زَوايا المُستطيل مُتساوية وتُساوي 90°.
- كلّ ضلعين مُتقابلين مُتوازيان.
- مجموع زوايا أيّ مستطيل يساوي 360°.
- مجموع مُربّع طول ضِلعين في مستطيل يساوي مربَّع القطر، وهذه النَّظريَّة تُعرف بنظرية فيثاغورس (بالإنجليزية: Phitagors theory)، وذلك لأنّ كلّ قطرٍ من أقطار المُستطيل يَنصف المُستطيل إلى مثلّثين مُتطابقين.
- كلّ مربع هو مستطيل وليس كلّ مستطيل مربع؛ لأنّ شَرط المُربّع أنه يتكون من أربعة أضلاع مُتساوية في الطول.
- قطرا أيّ مُستطيل متساويان، وينصفا بعضهما البعض.
- يَملك المُستطيل محوري تماثل، ومَركز تماثل واحد، وهو نُقطة تقاطع قطرية.
- يَملك المُستطيل جميع خواص متوازي الأضلاع.
حساب مساحة المستطيل
يتمّ حِساب مساحة المستطيل حسب ما هو معلوم منه كالتالي:[3]
- القانون الأول: إيجاد مساحة المستطيل إذا عُرِفَت كلٌّ من أبعاده، وهما الطول والعرض:
- القانون الثاني: إيجاد مساحة المستطيل إذا عُرِفَ مُحيط المستطيل وأحد أبعاده:
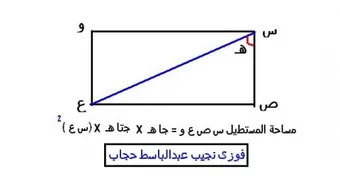
- القانون الثالث: إيجاد مساحة المستطيل إذا عُرِفَ طول أحد أبعاده، وطول قطره:
حساب محيط المستطيل
يتم حساب محيط المستطيل كالتالي:[3]
- القانون الأول: يُقاس محيط المستطيل إذا عُرِفَ كل من طوله وعرضه كالتالي:
- القانون الثاني: من الممكن إيجاد مُحيط المستطيل إذا علمت مساحة المستطيل، وطول أحد أضلاعه من خلال المعادلة التالية:
- القانون الثالث: من الممكن إيجاد مُحيط المستطيل إذا علم طول قطره، وطول أحد من أبعاده من خلال المعادلة التالية:
أمثلة على حساب مساحة المستطيل ومحيطه وقطره
- مثال (1): جد مساحة مُستطيل طوله 3سم، وعَرضه 5 سم.
الحل:
- مثال (2): جد مساحة متوازي الأضلاع، طوله 4 سم، وعَرضه ثلاثة أضعاف طوله.
الحل:
- مثال (3): جد طول قطر في مستطيل أبعاده: 3سم، 4 سم.
الحل:
- مثال (4): جد مساحة المستطيل، الذي يبلغ طول مُحيطه 12 سم، أمّا طوله فيبلغ 2 سم.
الحل:
أو:
- مثال (5): جد مساحة المستطيل الذي يبلغ طول قطره 15 سم، أما طوله فيبلغ 4 سم.
الحل:
أو:
- مثال (6): جد طول ضلع في مستطيل، محيطه 20 سم، وعرضه 6 سم.
الحل:
- مثال (7): جد قطر ومحيط المستطيل، الذي يَملك مساحة تساوي 20 سم²، وطول أحد أضلاعه 4 سم.
الحل:
- مثال (8): مثلثان متطابقان داخل مستطيل، طول كل من ضلعي القائمة لهما 3 سم، 4 سم. جد طول الضلع الثالث لهما.
الحل:
- مثال (9): جد مساحة مُستطيل طول أحد أضلاعه 3 سم، رُسِمَت خَارجه كرة، مَركزها هو مركز التّماثل للمستطيل، وتمسّ المستطيل عند رؤوسه الأربعهة، وقطرها 10 سم.
الحل:
المراجع
- ^ أ ب Math Open Reference Staff, "Rectangle"، Math Open Reference , Retrieved 2016-11-28. Edited.
- ↑ Web Math Staff, "Area of a Rectangle"، Web Math. Edited.
- ^ أ ب ت Online M School Staff, "Rectangle. Formulas and Properties of a Rectangle"، Online M School, Retrieved 2016-11-28. Edited.
