كيفية حساب مساحة المثلث
حساب مساحة المثلثلإيجاد مساحة أي مثلث (بالإنجليزية: Area of a Triangle) بشكل عام تقسم قاعدته على 2، ومن ثم يُضرب الناتج بارتفاعه. كما يمكن حساب مساحة المثلث
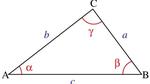
حساب مساحة المثلث
لإيجاد مساحة أي مثلث (بالإنجليزية: Area of a Triangle) بشكل عام تقسم قاعدته على 2، ومن ثم يُضرب الناتج بارتفاعه. كما يمكن حساب مساحة المثلث عبر معرفة زواياه وأضلاعه، وفي ما يأتي توضيح لبعض الحالات والقوانين التي تساعد على حساب المساحة باختلاف المعطى.[1][2]
إذا عُلم زاويتان وضلع في المثلث
إذا عُلم زاويتان وضلع فمن السهل حساب الزاوية الثالثة وذلك عن طريق صيغة مجموع زوايا المثلث، وهي: أ+ب+ج= 180، ولإيجاد الزاوية المجهولة (ج) تتبع المعادلة التالية: 180- (قياس الزاوية الأولى(أ)+ قياس الزاوية الثانية(ب))= قياس الزاوية المجهولة(ج). هذا فيما يخص إيجاد الزوايا، أما المساحة فيتم حسابها عن طريق اختيار أي ضلع من أضلاع المثلث (أب) وتربيع طوله، ومن ثم يُضرب مربع طوله بجيب الزاويتين المجاورتين لهذا الضلع (جيب كل زاوية على حدة)، وأخيراً يقسم على حاصل ضرب العدد 2 بجيب الزاوية المقابلة للضلع. ويعبر عن المساحة بالصيغة الآتية:[2]
إذا عُلم طولي ضلعين وزاوية محصورة بينهما
لحِساب مساحة مثلث إذا عُلم طول جانبين من جوانبه والزاوية المحصورة بينهما يُضرب طولي الضلعين المعلومين ببعضهما ومن ثم يُقسمان على العدد 2، وأخيراً يُضرب الناتج بجيب الزاوية المحصورة بينهما، وبمعنى آخر مساحة المثلث تساوي نصف حاصل ضرب طولي جانبي المثلث في جيب الزاوية. ويُعبّر عن المساحة بالصيغة الآتية:[2]
إذا عُلم أطوال الأضلاع الثلاثة
بما أن في هذه الحالة أطوال أضلاع المثلث جميعها معلومة ولا يوجد أي زاوية معلومة، يُستخدم ببساطة محيط المثلث لإيجاد مساحته، أي يتم إيجاد المساحة بدلالة المحيط، وكما هو معروف فإن محيط المثلث يُساوي مجموع أطوال جوانبه الثلاثة، ولإيجاد مساحة مثلث معلوم الأضلاع يقسم المحيط على العدد 2 لإيجاد نصفه، ومن ثم يُضرب بحاصل طرحه من طول كل ضلع، وأخيراً يؤخذ الجذر التربيعي للناتج، كما يمكن وضع إشارة الجذر التربيعي في البداية لتبسيط الحل. ويُعبَّر عن مساحة المثلث بالصيغة الآتية:[2]
أمثلة على كيفية إيجاد مساحة المثلث
- مثال1: أ ب ج مثلث فيه، الارتفاع يساوي 12سم، أما طول القاعدة فيساوي 20سم، جد مساحته.[3]
- مثال2: ثلاث دوائر متلاصقة من الخارج ببعضها البعض، بحيث رُسم مثلث يصل بين مراكزها الثلاث، فإذا كان نصف قطر كل دائرة على التوالي هو: (أ) 9سم، (ب) 5سم، (ج) 3سم، جد مساحة المثلث.[2]
- مثال3: غرفة مثلثة الشكل، فيها طول الضلع أ ب =10م، والضلع ب ج=7م، وقياس الزاوية ب= 25°، جد مساحتها.[3]
- مثال4: علبة خشبية قاعدتها مثلثة الشكل، إذا كان طول أحد أضلاعها يساوي 4سم، وقياس زوايا جوانب الضلع تساوي 65°، 35°، احسب مساحة قاعدة العلبة.
المراجع
- ↑ "Area of triangles", www.basic-mathematics.com. Edited.
- ^ أ ب ت ث ج بواسطة د. فرانك ايرز، د.روبرت موير، سلسلة ملخصات شوم ايزي ; حساب المثلثات، صفحة 117-121. بتصرّف.
- ^ أ ب "Area of Triangles Without Right Angles", www.mathsisfun.com. Edited.
ِ
المقال السابق: كيفية تنفيذ مشروع ناجح
المقال التالي: كيفية حفظ الورد الطبيعي
كيفية حساب مساحة المثلث: رأيكم يهمنا
0.0 / 5
0 تقييم
