التحويل من متر إلى قدم
التحويل من متر إلى قدميُمكن التحويل من وِحدة قياس الطول المعروفة بالمتر (m) إلى وِحدة قياس أخرى هي القدم (ft)؛ وذلك من خلال معرفة العلاقة بين هاتين الوحدتين،
تحويل الميل إلى كيلو
تحويل الميل إلى كيلوتُستخدم وحدة الميل (mi) كوحدة قياس في الولايات المتحدة الأمريكية، في حين تُستخدم وحدة الكيلومتر (km) في باقي أنحاء العالم، ويُمكن التحويل
تحويل الوزن
تحويل الوزن من كيلوغرام إلى باونديُمكن تحويل وزن جسم ما من الكيلوغرام إلى الباوند من خلال الضرب بمعامل التحويل وهو 2.2 باوند، أي أنّ كل كتلة وزنها واحد
تحويل القدم إلى متر
تحويل القدم إلى مترتُعتبر وحدة القدم (feet) أحد الوِحدات التي تُستخدم لقياس الطول أو المسافة في نظام وحدات القياس الأمريكي، ويُمكن التحويل من وحدة القدم إلى
تحويل الوحدات
تحويل وحدات الطوليوجد العديد من الوحدات التي تختص بقياس الطول، ومن هذه الوحدات: المليمتر، والسنتيمتر، والمتر، والكيلومتر،[1]
حساب محيط الدائرة
حساب محيط الدائرة باستخدام القطريُعرف محيط الدائرة بأنه عبارة عن المسافة التي تقع حول الشكل الدائري،[1] ويمكن حساب المحيط لدائرة ما من خلال معرفة قطرها، وذلك
حساب مساحة المثلث
حساب مساحة المثلث باستخدام طول القاعدة والارتفاعيمكن إيجاد المساحة باستخدام طول القاعدة والارتفاع بحيث تكون أطوالهما مُعطاة، ويتم بعد ذلك التطبيق على القاعدة
أفضل الطرق لحفظ جدول الضرب
فهم بعض مبادئ الضربيُمكن تسهيل عملية حفظ جدول الضرب من خلال فهم بعض المبادئ الرئيسة لهذه العملية الرياضية، ومن الخواص والمبادئ المهمة في عملية الضرب هو مبدأ
حساب مساحة المستطيل
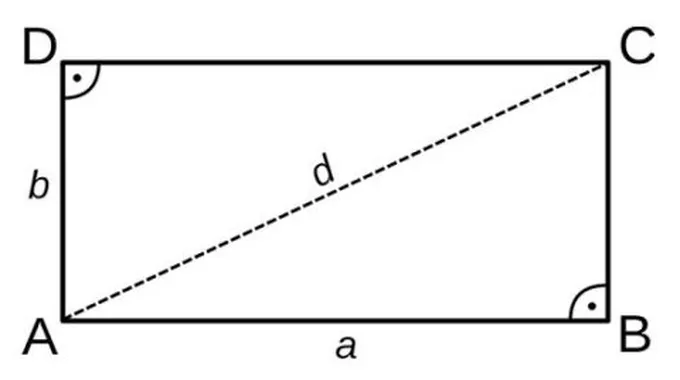
حساب مساحة المستطيليُعدّ المستطيل أحد أشهر الأشكال الهندسية الشائعة، وهو عبارة عن شكل له 4 جوانب متصلة مع بعضها البعض لها 4 زوايا قائمة، وكل جانبين متقابلين
حساب مساحة المثلث القائم
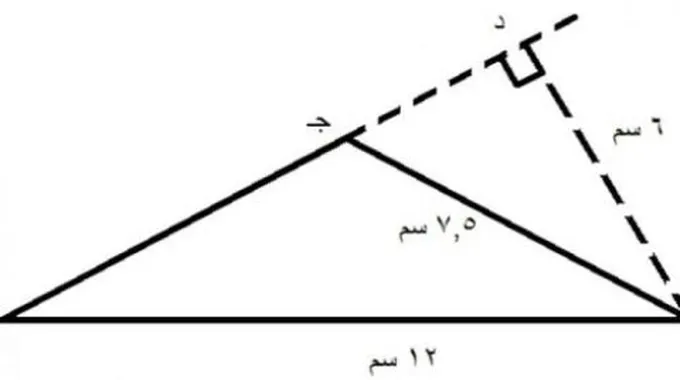
تعريف المثلث القائمالمثلث هو مضلع منتظم بثلاثة أضلاع يكون فيه مجموع ضلعين أكبر من الضلع الثالث، ويكون مجموع زواياه ْ180، أما المثلث القائم تكون إحدى زواياه
تحليل فرق بين مربعين
الصورة العامة للفرق بين مربعينيمكن إثبات الصورة العامة للفرق بين مربعين س² - ص²= (س+ص)*(س-ص) باستخدام طريقة فويل (بالإنجليزية: FOIL method) كما يأتي:[1]
حساب مساحة متوازي الأضلاع
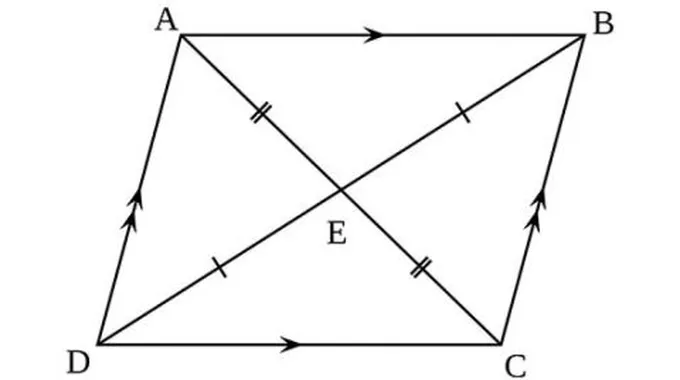
تعريف متوازي الأضلاع وخصائصهمتوازي الأضلاع هو شكل رباعي الأضلاع فيه كل ضلعين متقابلين متوازيين ويتميز بالخصائص الآتية:[1]
حساب مساحة شبه منحرف
مفهوم شبه المنحرفيتكون شبه المنحرف (بالإنجليزية: Trapezoid) من أربعة أضلاع وأربع زوايا، فيه ضلعان متقابلان ومتوازيان وهما قواعد شبه المنحرف، والضلعان الآخران
تحليل الفرق بين مربعين
الصيغة العامة لتحليل الفرق بين مربعينيعدّ اقتران الفرق بين مربعين حالة خاصة من الاقتران كثير الحدود، ويتكون من حدين مربعين بينهما إشارة طرح حسب الصيغة الآتية:
أدوات قياس الطول
أدوات قياس الطولالطرق المباشرةتستخدم عدة أدوات لقياس الأطوال التي يعلم بدايتها ونهايتها، وهي:[1]
تحليل المعادلة التربيعية
كتابة المعادلة التربيعيةتُستخدم طريقة تحليل العبارة التربيعية لحلّ أي معادلة رياضية من الدرجة الثانية والتي تكون على صيغة:
حل القسمة المطولة
شرح القسمة المطولةيمكن حل القسمة المطولة باتباع الخطوات الآتية:[1]
تحليل القوس التكعيبي
تحليل القوس التكعيبييتكون القوس التكعيبي من حدين أو أكثر مرفوع للقوة 3، ويُكتب على الصيغة الآتية:[1]
حساب ارتفاع المثلث
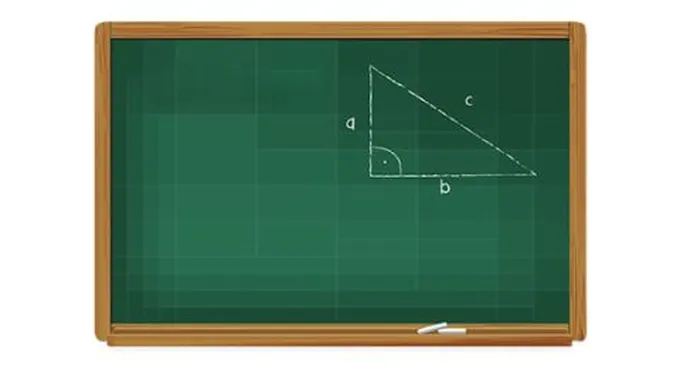
حساب ارتفاع المثلثالمثلث هو أحد الأشكال الهندسية المنتظمة التي تتكون من ثلاثة أضلاع، وثلاث زوايا، بحيث يكون مجموع زواياه 180°،وهناك ثلاثة أنواع من المثلثات؛
تحليل المتجهات
تحليل المتجهاتيُمكن إيجاد الإحداثي السيني (أس) والإحداثي الصادي (أص) للمتجه (أ) على النحو الآتي علماً بأنّ (أ) هي الوتر في المثلث القائم:[1]
تحليل العدد إلى عوامله الأولية
التحليل إلى العوامل الأوليةيقصد بالأعداد الأولية (بالإنجليزية: Prime Numbers) بأنّها الأعداد الأكبر من الرقم واحد، ولا تنتج من حاصل ضرب الأعداد ببعضها، مثل: 2،
ترتيب وحدات قياس الطول
وحدات قياس الطول في النظام المتريفيما يآتي وحدات قياس الطول في النظام المتري مرتبة من الأصغر إلى الأكبر:[1]
حل معادلة من الدرجة الأولى
حل معادلات من الدرجة الأولىتسمّى المعادلات من الدرجة الأولى بالمعادلات الخطيّة، وتكون صيغتها العامة كما يأتي: أس + ب = جـ، حيث إنّ أ، ب، جـ ثوابت، س متغير،
أسهل طريقة تعليم جدول الضرب
تمثيل جدول الضربيُمكن تسهيل عملية حفظ جدول الضرب وخاصة للأطفال من خلال التمثيل المادي لعمليات الضرب المُختلفة، ويُمكن استخدام أي شيء من الألعاب أو الكُتل
ارتفاع مثلث متساوي الساقين
ارتفاع المثلث متساوي الساقينيُعَد المثلث متساوي الساقين شكلاً هندسياً منتظماً يتكون من ثلاثة أضلاع، وثلاث زوايا، وتكون مجموع زواياه 180°، وقد سُمي بهذا الاسم
أهم أعمال الخوارزمي في الرياضيات
وضع القواعد الأساسية لعلم الجبرتُعدّ أطروحة الخوارزمي في الجبر من أهم أعماله المعروفة، وتُعرَف بكتاب المختصر في حساب الجبر والمقابلة، حيث تم دمج أجزاء من
أسرع طريقة لحفظ جدول الضرب كاملاً
قواعد عامة لحفظ جدول الضربيُمكن تطبيق بعض القواعد البسيطة لبعض الأرقام، والتي تساعد على حفظ جدول الضرب بشكل سريع، وفيما يأتي بعض من هذه القواعد:[1]
كيفية تبسيط الأعداد
تبسيط الأعداد باستخدام الصيغة العلميةيتم تبسيط الأعداد بتحويلها إلى الصيغة العلمية عند التعامل مع أرقام كبيرة جداً أو صغيرة جداً؛ بهدف الحفاظ على الوقت وتسهيل
كيفية تحويل الدقائق إلى ساعات
التحويل من دقائق إلى ساعاتتحتوي الساعة على ستين دقيقة، وبما أن عدد الدقائق في أي ساعة يكون ثابتاً وهو ستين دقيقة، فإنه يمكن تحويل أي من الدقائق إلى جزء من
كيفية إيجاد الوسيط
الوسيطيمثّل الوسيط أحد قيم النزعة المركزية، ويتم استخدامه لتحديد المتوسط التقريبي لمجموعة من البيانات، وتحديداً عندما يكون هناك قِيم كبيرة جداً أو قِيم صغيرة