كيفية حساب أضلاع المثلث القائم
استخدام نظرية فيثاغورسنظرية فيثاغورس هي نظرية تستخدم الهندسة الإقليدية لحساب أضلاع المثلث القائم، وتنص على أن مجموع مربعي ضلعي المثلث القائم يساوي مربع الوتر،
جدول الضرب
عملية الضربتعدّ عملية الضرب واحدة من العمليات الحسابية التي تُجرى على الأرقام، وتتكون من المضروب (multiplicand) والمضروب به (multiplier)، ويكون الناتج هو حاصل
حساب المعدل
المعدليعدّ المعدّل (بالإنجليزية: average) من الأمور التي تُستخدم بكثرة وبشكل يومي، فهو العدد الذي يتوسّط مجموعة من الأرقام، ويُطلق عليه في علم الإحصاء المتوسط
ما هو ميل المستقيم
تعريف ميل المستقيمالميل هو مفهوم مهم في علم الجبر، يمكن من خلاله معرفة اتجاه الخط المستقيم على محور س / ص، ويشير إلى مدى انحراف الخط المستقيم، كما يُعبر عن
ما هو قانون محيط المربع
قانون محيط المربعيُمكن تعريف محيط المربع بأنه طول الحدود التي تُحيط بالمربع، ويُكتب قانون محيط المربع بالصيغة الآتية:[1]محيط المربع= مجموع أطوال أضلاعه
ما هو قانون الفرق بين مكعبين
قانون الفرق بين مكعبينيُمكن تحليل الفرق بين مكعبين إلى حاصل ضرب حدين في ثلاثة حدود، وذلك كما يأتي:س3 - ص3= (س - ص)(س2 + س ص + ص2)، وتكون الإشارات كما يأتي:[1]
ما هو محيط المستطيل ومساحته
قانون محيط المستطيل ومساحتهمحيط المستطيل هو طول الحدود التي تحيط بالشكل، ويساوي مجموع أطوال أضلاعه الأربعة، فإذا كان طول المستطيل س، وعرضه ص، فإن محيط المستطيل
ما هو قانون مساحة الدائرة
قانون مساحة الدائرةتعرف مساحة الدائرة بأنها كمية المساحة التي تشغلها الدائرة، ويمكن التعبير عن مساحة الدائرة بالصيغة الآتية:[1]مساحة الدائرة= π × نق2.
ما هي مساحة المثلث
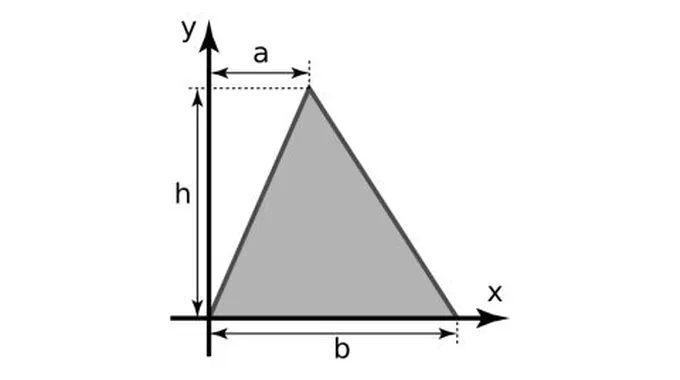
قوانين مساحة المثلثيمكن حساب مساحة المثلث باستخدام عدة قوانين كما يأتي:
ما هو محيط المثلث ومساحته
محيط المثلث ومساحتهتُعرف مساحة المضلع بأنها عدد الوحدات المربعة التي توجد داخل المضلع، ومن الجدير بالذكر أن المساحة تمثل اتجاهين في أي مستوى، ويعرف المثلث بأنه
ما هو قانون المربع
قوانين المربعالمربع هو شكل رباعي الأضلاع، تكون جميع أضلاعه متساوية، وجميع زواياه الأربعة قوائم، وقوانينه هي كالآتي:[1]
ما هو محيط الدائرة ومساحتها
محيط الدائرةيُعرف محيط الدائرة بأنه المسافة المحيطة بالدائرة،[1] ويُعطى بالعلاقة الآتية:[2]محيط الدائرة = π × القطر.أو محيط الدائرة = 2 × π× نصف القطر.
ما هو محيط ومساحة الدائرة
تعريف محيط الدائرة ومساحتهاقبل البدء بحساب محيط بالدائرة ومساحتها لا بد من تعريف بعض المصطلحات المهمة:[1]
ما هو قانون جيب التمام
قانون جيب التماميُمكن باستخدام قانون جيب التمام حل العديد من المشاكل التي تتعلق بالمثلثات، وهناك عدة أشكال لقانون جيب التمام، وهي:[1]
ما هو قانون محيط متوازي الأضلاع
قانون محيط متوازي الأضلاعمتوازي الأضلاع هو عبارة عن مستطيل مائل، يكون فيه كل ضلعين متقابلين متساويين مثل المستطيل، بالإضافة إلى ذلك فإن كل ضلعين متقابلين فيه
ما هو قياس الزاوية الحادة
تحديد نوع الزاويةقبل البِدء بالطُرق المُتّبعة لقياس الزوايا، لا بد من تحديد نوع الزاوية الموجودة، وفيما يأتي الأشكال الأربعة للزوايا الأكثر شيوعاً في عالم
ما هو قانون حجم الاسطوانة
قانون حجم الأسطوانةالأسطوانة عبارة عن مادة صلبة تتكون من دائرتين مُتطابقتين في مستويين مُتوازيين، وجميع الخطوط التي تُكوّن الأسطوانة تكون موازية للمركز المقابل
ما هو قانون حجم الكرة
قانون حجم الكرةيُمكن تعريف الكرة بأنها شكل دائري يوجد في ثلاثة أبعاد، ويُعطى قانون حجم الكرة بالعلاقة الآتية:[1]حجم الكرة = (4/3) × π × نق3.وفي بعض الحالات
تحليل مجموع مكعبين
تحليل مجموع مكعبينيمكن كتابة الصيغة العامة لمجموع المكعبين على النحو الآتي:[1]أ3 + ب3 = (أ + ب)(أ2 - أ ب + ب2).
ما هو ميل الخط المستقيم
ميل الخط المستقيميُعرف ميل الخط المستقيم بأنه قيمة يتم من خلالها قياس مدى انحدار الخط المستقيم، ويرمز له بالرمز م، ويمثل التغيّر في قيم الصادات بالنسبة لقيم
ما هو علم الجبر في الرياضيات
علم الجبريُعرف علم الجبر بأنه أحد أهم فروع علم الرياضيات، ويقوم على مبدأ المُعادلات التي تتكون من مجموعة من المُتغيّرات والثوابت؛ بحيث تكون الثوابت عبارة عن
ما هو قانون حجم المخروط
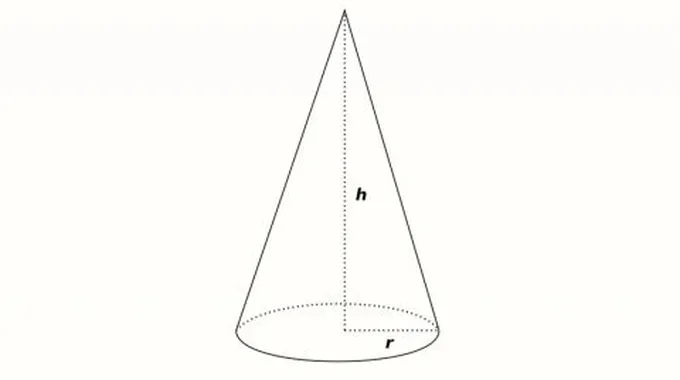
قانون حجم المخروطيُعرف حجم المخروط بأنه مقدار الحيز الذي يشغله في ثلاثة أبعاد، ويُقاس بالعديد من الوحدات مثل إنش3، قدم3، سم3، م3، ويُعرف حجم المخروط بأنه ثُلث
حل المعادلة التربيعية
استخدام طريقة التحليل إلى العواملالمعادلة التربيعية هي المعادلة التي تأتي بالصيغة الآتية: أس2+ب س-جـ=صفر؛ حيث إنّ: أ، ب، جـ ثوابت، وتعتبر طريقة التحليل إلى
ما هو نصف قطر الدائرة
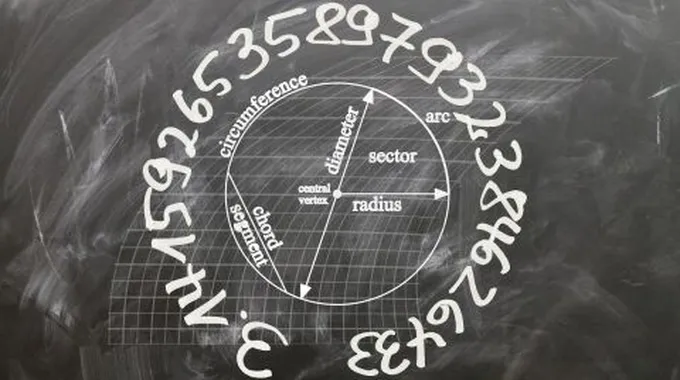
نصف قطر الدائرةالدائرة هي شكل مُستدير تماماً بشكل مثالي، ولكل دائرة مركز يقع في مُنتصفها، ويُمكن القول بأن الدائرة هي أي شكل تكون فيه المسافة بين مركزها وأي
ما هو قانون نصف قطر الدائرة
نصف قطر الدائرةيُعرف نصف القطر على أنه المسافة من مركز الدائرة إلى محيطها الخارجي، بينما يُعرف قطرها على أنه الخط الممتد عبر الدائرة ماراً بمركزها، أما محيط
ما هو قانون قطر المربع
قانون قطر المربعقطر المربع عبارة عن خط مستقيم يربط بين إحدى زوايا المربع، والزاوية المقابلة له، ويمكن استخدام نظرية فيثاغورس لإيجاد طول قطر المربع، حيث إن قطر
ما هي معادلة المستقيم
معادلة المستقيميُمكن اشتقاق معادلة الخط المستقيم للنقطتين (س1، ص1)، و (س2، ص2) باتباع الخطوات الآتية:[1]
ما هي معادلة الخط المستقيم
معادلة الخط المستقيميتم التعبير عن معادلة الخط المستقيم من خلال الصيغة الآتية:[1]ص = أس + ب، حيث إنّ:
ما هو قانون طول قطر المربع
قانون طول قطر المربعالمربع له قطران، وكل قطر يمثل الخط المرسوم بين إحدى زوايا المربع، والزاوية المقابلة لها، ويتميز قطر المربع بالخصائص الآتية:[1]
كيفية إيجاد طول قطر المربع
طول قطر المربعيحتوي المربع على قطرين متساويين في الطول، وينصفان بعضهما البعض عند نقطة المُنتصف، ويمكن حساب طول قطر المربع من خلال إيجاد حاصل ضرب طول الضلع