تحليل مجموع مكعبين
تحليل مجموع مكعبينيمكن كتابة الصيغة العامة لمجموع المكعبين على النحو الآتي:[1]أ3 + ب3 = (أ + ب)(أ2 - أ ب + ب2).
ما هو قانون حجم الكرة
قانون حجم الكرةيُمكن تعريف الكرة بأنها شكل دائري يوجد في ثلاثة أبعاد، ويُعطى قانون حجم الكرة بالعلاقة الآتية:[1]حجم الكرة = (4/3) × π × نق3.وفي بعض الحالات
ما هو قانون حجم الاسطوانة
قانون حجم الأسطوانةالأسطوانة عبارة عن مادة صلبة تتكون من دائرتين مُتطابقتين في مستويين مُتوازيين، وجميع الخطوط التي تُكوّن الأسطوانة تكون موازية للمركز المقابل
ما هو قياس الزاوية الحادة
تحديد نوع الزاويةقبل البِدء بالطُرق المُتّبعة لقياس الزوايا، لا بد من تحديد نوع الزاوية الموجودة، وفيما يأتي الأشكال الأربعة للزوايا الأكثر شيوعاً في عالم
ما هو قانون محيط متوازي الأضلاع
قانون محيط متوازي الأضلاعمتوازي الأضلاع هو عبارة عن مستطيل مائل، يكون فيه كل ضلعين متقابلين متساويين مثل المستطيل، بالإضافة إلى ذلك فإن كل ضلعين متقابلين فيه
ما هو قانون جيب التمام
قانون جيب التماميُمكن باستخدام قانون جيب التمام حل العديد من المشاكل التي تتعلق بالمثلثات، وهناك عدة أشكال لقانون جيب التمام، وهي:[1]
ما هو محيط ومساحة الدائرة
تعريف محيط الدائرة ومساحتهاقبل البدء بحساب محيط بالدائرة ومساحتها لا بد من تعريف بعض المصطلحات المهمة:[1]
ما هو محيط الدائرة ومساحتها
محيط الدائرةيُعرف محيط الدائرة بأنه المسافة المحيطة بالدائرة،[1] ويُعطى بالعلاقة الآتية:[2]محيط الدائرة = π × القطر.أو محيط الدائرة = 2 × π× نصف القطر.
ما هو قانون المربع
قوانين المربعالمربع هو شكل رباعي الأضلاع، تكون جميع أضلاعه متساوية، وجميع زواياه الأربعة قوائم، وقوانينه هي كالآتي:[1]
ما هو محيط المثلث ومساحته
محيط المثلث ومساحتهتُعرف مساحة المضلع بأنها عدد الوحدات المربعة التي توجد داخل المضلع، ومن الجدير بالذكر أن المساحة تمثل اتجاهين في أي مستوى، ويعرف المثلث بأنه
ما هي مساحة المثلث
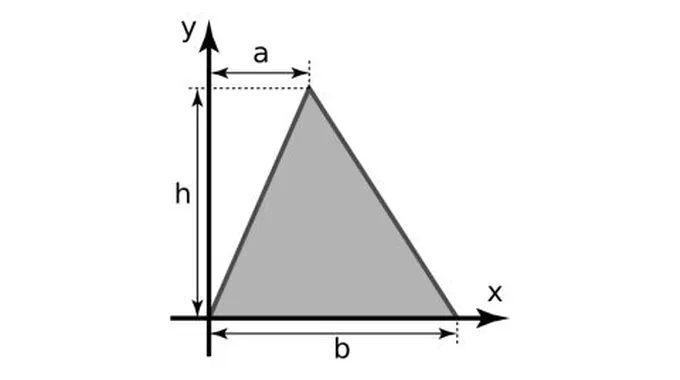
قوانين مساحة المثلثيمكن حساب مساحة المثلث باستخدام عدة قوانين كما يأتي:
ما هو قانون مساحة الدائرة
قانون مساحة الدائرةتعرف مساحة الدائرة بأنها كمية المساحة التي تشغلها الدائرة، ويمكن التعبير عن مساحة الدائرة بالصيغة الآتية:[1]مساحة الدائرة= π × نق2.
ما هو محيط المستطيل ومساحته
قانون محيط المستطيل ومساحتهمحيط المستطيل هو طول الحدود التي تحيط بالشكل، ويساوي مجموع أطوال أضلاعه الأربعة، فإذا كان طول المستطيل س، وعرضه ص، فإن محيط المستطيل
ما هو قانون الفرق بين مكعبين
قانون الفرق بين مكعبينيُمكن تحليل الفرق بين مكعبين إلى حاصل ضرب حدين في ثلاثة حدود، وذلك كما يأتي:س3 - ص3= (س - ص)(س2 + س ص + ص2)، وتكون الإشارات كما يأتي:[1]
ما هو قانون محيط المربع
قانون محيط المربعيُمكن تعريف محيط المربع بأنه طول الحدود التي تُحيط بالمربع، ويُكتب قانون محيط المربع بالصيغة الآتية:[1]محيط المربع= مجموع أطوال أضلاعه
ما هو ميل المستقيم
تعريف ميل المستقيمالميل هو مفهوم مهم في علم الجبر، يمكن من خلاله معرفة اتجاه الخط المستقيم على محور س / ص، ويشير إلى مدى انحراف الخط المستقيم، كما يُعبر عن
حساب المعدل
المعدليعدّ المعدّل (بالإنجليزية: average) من الأمور التي تُستخدم بكثرة وبشكل يومي، فهو العدد الذي يتوسّط مجموعة من الأرقام، ويُطلق عليه في علم الإحصاء المتوسط
جدول الضرب
عملية الضربتعدّ عملية الضرب واحدة من العمليات الحسابية التي تُجرى على الأرقام، وتتكون من المضروب (multiplicand) والمضروب به (multiplier)، ويكون الناتج هو حاصل
كيفية حساب أضلاع المثلث القائم
استخدام نظرية فيثاغورسنظرية فيثاغورس هي نظرية تستخدم الهندسة الإقليدية لحساب أضلاع المثلث القائم، وتنص على أن مجموع مربعي ضلعي المثلث القائم يساوي مربع الوتر،
تحليل العبارة التربيعية
خطوات تحليل العبارة التربيعيةيتم تحليل العبارة التربيعية التي تكون على الصورة أس2 + ب س + جـ = 0، باستخدام الخطوات الآتية:
كيفية استخراج الوسط الحسابي
طريقة حساب الوسط الحسابيلإيجاد الوسط الحسابي لمجموعة من الأرقام يتم جمع هذه الأرقام ثم القسمة على عددها، وذلك على النحو الآتي:في حال وجود هذه المجموعة من
كيفية إيجاد الوسيط
الوسيطيمثّل الوسيط أحد قيم النزعة المركزية، ويتم استخدامه لتحديد المتوسط التقريبي لمجموعة من البيانات، وتحديداً عندما يكون هناك قِيم كبيرة جداً أو قِيم صغيرة
كيفية تحويل الدقائق إلى ساعات
التحويل من دقائق إلى ساعاتتحتوي الساعة على ستين دقيقة، وبما أن عدد الدقائق في أي ساعة يكون ثابتاً وهو ستين دقيقة، فإنه يمكن تحويل أي من الدقائق إلى جزء من
كيفية تبسيط الأعداد
تبسيط الأعداد باستخدام الصيغة العلميةيتم تبسيط الأعداد بتحويلها إلى الصيغة العلمية عند التعامل مع أرقام كبيرة جداً أو صغيرة جداً؛ بهدف الحفاظ على الوقت وتسهيل
كيفية إيجاد النسبة المئوية
كيفية إيجاد النسبة المئوية لإيجاد النسبة المئوية من عدد ما، يجب أن يكون اثنان من النسبة، أو الجزء والكمية الكلية معلومين، ويمكن بعد ذلك حساب النسبة المئوية
كيفية حساب الضريبة
كيفيّة حساب الضريبةأحد أهمّ أنواع الضرائب التي تفرضها الدولة على أفرادها هي ضريبة الدخل، وتُحدد قيمتها من قيمة الدخل الذي يجنيه الفرد سنوياً، حيث يتمّ تقسيم
كيفية حساب كمية المادة
كيفية حساب كمية المادةيمكنُ حسابُ الصيغة النسبية لكمية المادّة ضمن مُركّب معيّن، من خلال جمع كلٍّ من الكتل الذرية النسبية مع بعضها للذرات المشتركة في تركيب
كيفية حساب الرطوبة النسبية
كيفية حساب الرطوبة النسبيةيمكنُ حسابُ الرطوبة النسبية من خلال تجربة عملية بسيطة، باستخدام مقياس الحرارة الثنائي (الرطب/ الجاف)، والذي يُطلق عليه تسمية
ما هي مضاعفات العدد 10
مضاعفات العدد 10المضاعف هو نتيجة ضرب العدد بعدد آخر صحيح، وليس بعدد كسري.[1] وللمضاعفات تطبيقات كثيرة في الرياضيات: في حساب المضاعف المشترك الأصغر،[2] وفي
ما هي مساحة المستطيل
مساحة المستطيلمساحة المستطيل هي قيمة سطح الشكل،[1]، أي المساحة التي تغطية والتي توجد عادةً للاشكال الهندسيّة الموجودة في بُعدين، وتقاس بوحدة مربّعة، [2] ويمكن