قانون ضعف الزاوية
قانون ضعف الزاويةلقانون ضعف الزاوية أشكال متعددة مرتبطة بالاقترانات المثلثية الثلاث، وهذه الأشكال هي:[1]
بحث عن كثيرات الحدود
تعريف كثيرات الحدوديمكن تعريف كثيرات الحدود على أنّها عبارة عن تعبيرات رياضية تتكون من متغيرات ومعاملات، بالإضافة إلى عمليات الجمع والطرح والضرب والأسس غير
قانون الجيب
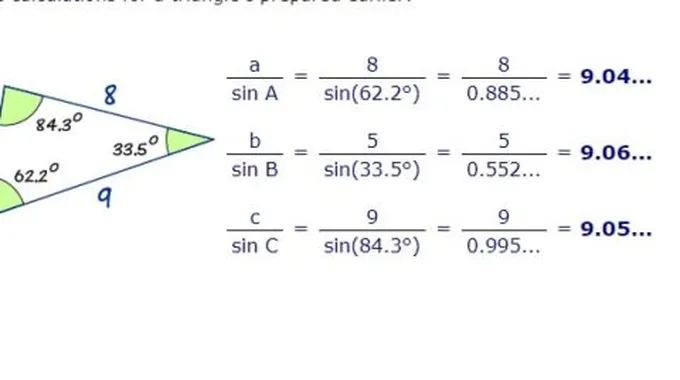
قانون الجيبيعد قانون الجيب أحد القوانين المفيدة في حل المثلثات، وهو يستخدم في جميع أنواع المثلثات، وصيغة هذا القانون هي: (أ/جا أَ=ب/جابَ=ج/جا جَ)، حيث ثمثل
قانون طول قطر الدائرة
قانون طول قطر الدائرةيوضح قانون قطر الدائرة العلاقة بين نصف قطر الدائرة وقطرها، حيث يتكون قطر الدائرة من قطعتين يُطلق على كل منهما اسم نصف القطر، ومن الجدير
خصائص الضرب
خصائص الضربفي هذا المقال سنناقش ثلاث خصائص مهمة ورئيسية لأحد العمليات الرياضية المهمة (الضرب)، وهذه الخصائص كالتالي:[1]
طرق حل المعادلة الأسية
طرق حل المعادلة الأسيةعند التعامل مع معادلة أُسِّية مثل هذه المعادلة (4x=16) حيث الحرف x يمثل الأس (القوة) المقرونة بالعدد 4، فإنّ السؤال الذي يتبادر لذهن
طرق حل المعادلة التربيعية
طرق حل المعادلة التربيعيةسنتطرق لأحد طرق حل المعادلة التربيعية والتي تدعى بطريقة إكمال المربع، حيث تتعدد طرق المعادلة التربيعية مثل أخذ الجذر التربيعي و إيجاد
قسمة عدد على صفر
قسمة عدد على صفرلا يُوجَدُ أيُّ جواب للسؤال الذي يُطرَح عن ناتج قسمة عدد ما على العدد صفر، حيثُ إنّه لا يوجد معنى للتعبير الرياضيّ لقسمة أيّ عدد على صفر على
تعريف عملية الضرب
تعريف عمليّة الضّربيُشيرُ مفهوم عمليّة الضّرب في الحساب الأوليّ إلى عمليّات الجمع المتتاليّة، كما أنّها عمليّة حسابيّة مُعاكسة لعمليّة القسمة، ويُطلق على حديّ
ما هي زاوية الميل
زاوية الميليُمكن اعتبارُ زاوية الميل تلك الزاويةَ المنحصرةَ بين خط أفقي وخط مائل، حيث يُعبّر عن قيمة ميل هذه الزاوية، والذي يعتبر السِّمة الأهم لها، من خلال
خواص الجمع
الخاصيّة التبادليّةيُطلق على الخاصيّة الرياضيّة التي توضّح أنّ: (ناتج عمليّة جمع عددين متساوٍ؛ بِغَض النّظر عن ترتيب الأعداد المُضافة) اسم الخاصيّة التبادليّة
القسمة المطولة
القِسمة المُطوّلةيُمكن تبسيط الأرقام البسيطة، أو المُعقّدة إلى خطواتٍ بسيطةٍ عن طريق عمليّة حسابيّةٍ تُسمّى القسمة المطوّلة (بالإنجليزيّة: Long Division)،
خصائص عملية جمع الأعداد الحقيقية
الخاصيّة التبادليّةإنّ ترتيب الأعداد الحقيقيّة أثناء إجراء عمليّة الجمع لا يغيّر النتيجة؛ حيث إنّ عمليّة الجمع في علم الجبر تبادليّة، وبالتّالي لن تتغيّر نتيجة
طريقة حساب زكاة الأسهم
طريقة حساب زكاة أسهُم الاستثمار والأسهُم المتاجر بهاسنتطرق فيما يلي إلى كيفية إخراج زكاة الأسهُم التي يتاجر بها المرء وزكاة الأسهُم التي يُستثمر بها، وهي على
خواص الأعداد
خواص الأعداد الحقيقةإذا كانت الأعداد المرموز لها بالرموز أ، ب، ج هي أعداد حقيقية، فيُمكن توضيح بعض الخصائص لهذه الأعداد وكما يلي:[1]
طريقة تحفيظ الأطفال جدول الضرب
تمثيل جدول الضربيُمكن تحفيظ الأطفال لجدول الضرب من خلال استخدام أسلوب الإسقاط الواقعي لمسألة ضرب مُعينة وتمثيلها بحيث يستطيع الطفل أن يفهم معنى الضرب من خلال
كيف أتعلم عملية القسمة
القِسمة الطويلةإن عملية القِسمة الطويلة هي عملية مشابهة لتلك القسمة العادية القصيرة، إلا أنه في عملية القسمة المطولة ينتُج لدينا باقي طويل نسبة إلى عملية
خواص القوى في الرياضيات
خواص القوى في الرياضياتفيما يلي نذكر الخصائص المُتعلقة بالقوى (الأُسُس) في الرياضيات وهي كالآتي:[1]
شرح كيفية حساب المعدل التراكمي
كيفيّة حِساب المُعدّل التّراكميّيُمثّل الرّقم الناتج عن عمليّة تقسيم مجموع النّقاط الكليّة المُكتسبة في برنامجٍ ما على المجموع الكليّ لعدد السّاعات المُنجزة،
شرح طرح الأعداد الصحيحة
كيفيّة طرح الأعداد الصحيحةإنّ المبدأ الرئيسيّ في عمليّة طرح الأعداد الصحيحة هو تحويل عمليّة طرح الأعداد الصحيحة إلى عمليّة جمع الأعداد الصحيحة كما يلي:[1]
طريقة حساب مساحة الغرفة
طريقة حِساب مساحة الغُرفةحِساب مساحة الغُرفة مُنتظمة الشّكلتكون طريقة حِساب المساحة عمليةً بسيطةً جداً، في الغرف التي تتّخذ شكل المربّع، أو المُستطيل، وما يلي
طرق حل المعادلات الجبرية
كيفيّة حل المُعادلة الجبريّةإنّ حل المُعادلة الجبريّة هو الرّقم الذي يُمكن وضعه مكان المُتغيّر لإنتاج تعبيراً صحيحاً، وعلى الرّغم من عدم وجود طريقة مثاليّة لحل
كم عدد أضلاع المكعب
عدد أضلاع المُكعّبيبلُغ عدد أضلاع المُكعّب اثنا عشرة ضِلعاً أو حافةً، وتتميّز أضلاع المُكعّب بأنّها متساويةً بالطّول وذلك لأنّ جميع وجوهه مُربّعة الشّكل،
طريقة حساب قطر الدائرة
طريقة حساب قُطر الدّائرةيُمكن حساب قطر الدّائرة عن طريق ضرب نصف القطر بالعدد2، أي 2*نصف القطر، أو 2*نق، كما يُمكن حسابه عن طريق حساب طول الخط الذي يقطع مركز
كيف يحسب المعدل الجامعي
كيفيّة حساب المُعدّل الجامعييُمثّل الرّقم الذ ينتُج عن إجراء عمليّة القسمة لمجموع النّقاط الكليّة التي حصل عليها الطّالب في برنامجٍ ما على المجموع الكليّ لعدد
شرح عملية القسمة
شرح عمليّة القِسمة القصيرةإنّ الأساس في عمليّة القسمة هو توزيع أجزاءاً متساويةً على مجموعةٍ من الأشياء أو الأشخاص، وما يلي أمثلة على إجراء عمليّة القسمة:[1]
خصائص الجمع وقواعد الطرح
خصائصُ جمعِ الأعدادعملية جمع الأعداد هي عملية تعبّر عن إضافة قيمة عدد إلى قيمة عدد آخر لينتج عدد جديد، وتخضع عملية جمع الأعداد إلى العديد من القواعد التي يجب
شرح رموز الرياضيات
رُموز الرياضياتتمتلك رُموز الرياضيات أهمية كبيرة في حياتنا اليومية، حيث من الممكن أن نقوم باستخدامها حتى دون انتباه، في البقالة مثلاً أو البنك وغيرها، وتمتاز
خصائص الاقتران الخطي
الاقتران الخطيالاقتران الخطي هو معادلة لخط مُستقيم، يكون له الشكل العام بناءاً على هذا الشكل:[1]
شرح قانون النسب المتضاعفة
شرح قانون النِسَب المُتضاعفةينص قانون النِسَب المُتضاعفة على أن المُركب الذي ينتج من اتحاد عنصرين كيماويين مع بعضهما البعض فإن النسبة بين الكتل المختلفة من أحد