ما هو قانون طول ضلع المربع
قانون طول ضلع المربعالمربع هو مضلع رباعي تكون جميع أضلاعه الأربعة متساوية، وجميع زواياه قوائم، ويكون فيه كل ضلعين متقابلين متوازيين ومتساويين، ويمكن حساب طول
ما هو قطر المستطيل
قطر المستطيليحتوي المستطيل على قُطرين، ويُعرف القطر بأنه خط مستقيم يصل بين رؤوس المستقيم المُتقابلة، وتتميز أقطار المستطيل بالخصائص الآتية:[1]
ما هو قانون محيط المعين
قانون محيط المعينالمعين هو شكل مسطح له أربعة أضلاع، وأربع زوايا لا يُشترط أن تكون قياساتها 90 درجة، ويعرف محيط المعين بأنه المسافة الكلية التي تحيط بالشكل
ما هو قانون مساحة متوازي الاضلاع
مساحة متوازي الأضلاعتُعرف مساحة المُضلّع بأنها عدد الوِحدات المربعة التي توجد داخل المضلع، ومن الجدير بالذكر بأن المساحة تُمثّل بُعدَين، ومتوازي الأضلاع يتكون
ما هو قطر المربع
قطر المربعيحتوي المربع على قطرين، ويمكن تعريف القطر في المربع بأنه قطعة مُستقيمة تربط بين كل زاويتين من زوايا المربع المتقابلة، وتتميز أقطار المربع بالخصائص
ما هو قانون حجم المكعب
قانون حجم المكعبيُعرف المكعب بأنه عبارة عن شكل ثُلاثي الأبعاد، يتكون عندما ترتبط ستة مربعات مُتماثلة ببعضها البعض مكونةً شكلاً مُغلقاً، ويحتوي المكعب على ستة
ما هو قانون طول قطر المستطيل
قانون طول قطر المستطيلالمستطيل له قطران متساويان في الطول، وينصفان بعضهما البعض عند نقطة المنتصف،[1] ولإيجاد طول قطر المستطيل فإنه يتم قسمة المستطيل إلى مثلثين
ما هو علم التفاضل والتكامل
علم التفاضل والتكامليُطلق على علم التفاضل والتكامل اسم الكالكولس (بالإنجليزيّة: Calculus)، ويمكن تعريفه على أنه أحد فروع الرياضيات الذي يتعامل مع إيجاد
كيفية إيجاد القاسم المشترك الأكبر لثلاثة أعداد
إيجاد القاسم المشترك الأكبر لثلاثة أرقاميُمكن تعريف العامل المُشترك الأكبر أو القاسم المشترك الأكبر بأنه أكبر رقم صحيح بين العوامل لمجموعة من الأرقام، وتَكمُن
ما هو قانون الميل
قانون الميليُعطى قانون ميل الخط المستقيم بالصيغة الآتية:[1]الميل = فرق الصادات / فرق السينات= ص2 - ص1 / س2 - س1، حيث إنّ:(س1، ص1) و (س2، ص2) هما إحداثيات
ما هو قانون محيط الكرة
قانون محيط الكرةتعرف الكرة بأنها جسم متماثل ثلاثي الأبعاد دائري الشكل، ويسمى الخط الذي يربط بين المركز وحدود الدائرة نصف القطر، ويطلق على أطول خط مستقيم يمر
ارتفاع المعين
ارتفاع المعينيُعرف ارتفاع المعين بأنه المسافة الواصلة بين ضلعَي المعين المُتقابلين، والذي يصنع زاوية قائمة مع الضلعين، والمعين عبارة عن شكل رُباعي مُتساوي
كيفية إيجاد طول قطر المربع
طول قطر المربعيحتوي المربع على قطرين متساويين في الطول، وينصفان بعضهما البعض عند نقطة المُنتصف، ويمكن حساب طول قطر المربع من خلال إيجاد حاصل ضرب طول الضلع
ما هو قانون طول قطر المربع
قانون طول قطر المربعالمربع له قطران، وكل قطر يمثل الخط المرسوم بين إحدى زوايا المربع، والزاوية المقابلة لها، ويتميز قطر المربع بالخصائص الآتية:[1]
ما هو علم الرياضيات
علم الرياضياتيُعرف علم الرياضيات بأنه العلم الذي يتعامل مع الأشكال والكميات، وكيفية ترتيبها، وهو العنصر الأساسي لكل شيء في الحياة اليومية، بما في ذلك الأجهزة
ما هو قانون نصف قطر الدائرة
نصف قطر الدائرةيُعرف نصف القطر على أنه المسافة من مركز الدائرة إلى محيطها الخارجي، بينما يُعرف قطرها على أنه الخط الممتد عبر الدائرة ماراً بمركزها، أما محيط
ما هي معادلة الخط المستقيم
معادلة الخط المستقيميتم التعبير عن معادلة الخط المستقيم من خلال الصيغة الآتية:[1]ص = أس + ب، حيث إنّ:
ما هي معادلة المستقيم
معادلة المستقيميُمكن اشتقاق معادلة الخط المستقيم للنقطتين (س1، ص1)، و (س2، ص2) باتباع الخطوات الآتية:[1]
ما هو قانون قطر المربع
قانون قطر المربعقطر المربع عبارة عن خط مستقيم يربط بين إحدى زوايا المربع، والزاوية المقابلة له، ويمكن استخدام نظرية فيثاغورس لإيجاد طول قطر المربع، حيث إن قطر
ما قانون حجم المكعب
حجم المكعبيُعرف حجم المكعب بأنه كمية المادة الموجودة داخل المكعب، وعند التعامل مع الحجم يتم استخدام وحدات مكعبة، والسبب في ذلك بأن الحجم يعتمد على الأبعاد
كيفية إيجاد طول ضلع المربع
قانون طول ضلع المربع المربع هو شكل هندسي، ويُعدّ حالة خاصة من المستطيل، إذ يحتوي على أربعة أضلاع، وجميع زواياه قوائم، لكن جميع أضلاعه الأربعة تكون متساوية، وفي
ما قانون حجم الكرة
قانون حجم الكرةيعرف الحجم بأنه كمية المادة التي تشغل مساحة وحيزاً، وتقاس بالوحدات المكعبة مثل قدم3، وإنش3، وسم3، وم3، ومن الجدير بالذكر أنه يجب التأكد من تماثل
كيفية إيجاد طول وعرض المستطيل
إيجاد طول وعرض المستطيلباستخدام مساحة المستطيليُمكن إيجاد مساحة المستطيل من خلال معرفة طوله وعرضه، وتجدر الإشارة إلى أن الطول والعرض عبارة عن قيمتين مستقلتين،
ارتفاع متوازي الاضلاع
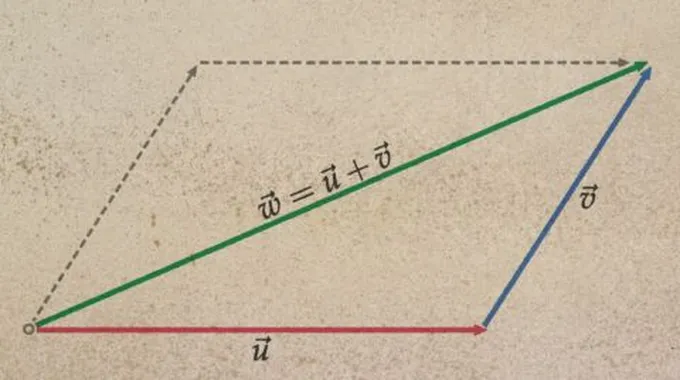
ارتفاع متوازي الأضلاعلإيجاد ارتفاع متوازي الأضلاع يتمّ الحاجة إلى تعريف كل من ارتفاع، وقاعدة، ومساحة متوازي الأضلاع، ويُعرف متوازي الأضلاع بأنّه شكل رباعي يكون
ما هو قانون ارتفاع المثلث
إيجاد ارتفاع المثلثباستخدام المساحةمساحة المثلث = (2/1) × طول القاعدة × الارتفاع، وبالتالي فإن ارتفاع المثلث يساوي:[1](2 × مساحة المثلث) / طول القاعدة.
ارتفاع المثلث القائم
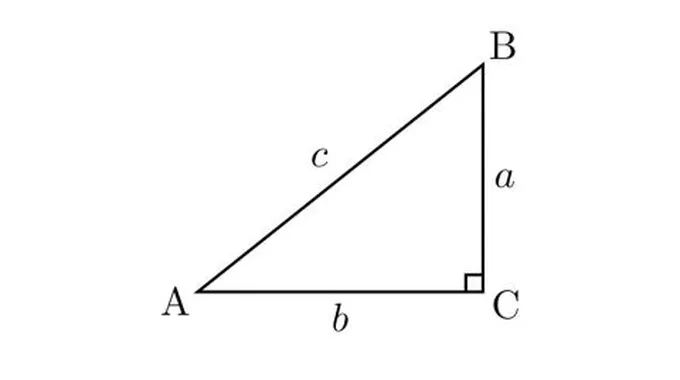
ارتفاع المثلث القائم باستخدام المساحةفي بعض الأحيان فإن مساحة المثلث، وقاعدته تكون معروفة، أما ارتفاعه فهو غير معروف، وبالتالي يمكن الحصول على الارتفاع من خلال